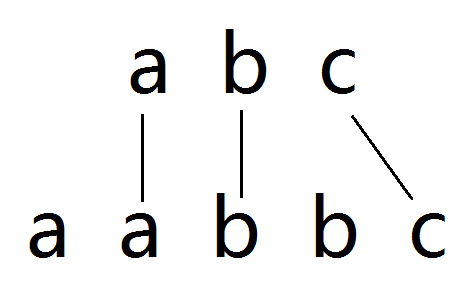$Aguin$ has one string $A$ with the length of $n$ and one string $B$ with the length of $m$. Both of them contains only lowercase letters. But the strings are such antiques that some characters can't be recognized (replaced with '$*$'), and it can be any lowercase letters.
Now $Aguin$ is wondering whether $A$ is a substring of $B$. However, his way of match is a little strange. The detailed rules for match are as follows : the beginning of the $A$ is aligned with the $i^{th}$ character of the $B$, and every character in the $A$ can find the same one in $B$, and the position deviation does not exceed the $k$, then it is considered that $A$ is matched with $B$ in the subordinate position of the $B$. That is to say, for all $j (1 \leq j \leq |A|)$, there is a $p (1 \leq p \leq |B|)$, which satisfies $|j-(p-i+1)| \leq k$, $i+j \leq m$ and $A[j]=B[p]$.
For example, string $"abc"$ can be matched in the $2^{nd}$ location of $"aabbc"$.
And if $k=0$, string "***" can be matched with any other strings which length is $3$.
Given strings $A$, $B$ and the number $k$, you are supposed to find how many locations can $A$ be matched in $B$.