3143: 彩虹岛只下围棋

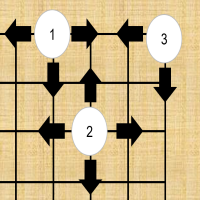
棋盘上有纵横各$n、m$条等距，垂直交叉的平行线，构成n*m个交叉点。对局双方各执一色棋子，黑先白后，交替下子，每次只能下一子。棋子在棋盘上，与它直线紧邻的空点是这个棋子的气，如图$（c）$所示，白棋1有三口气，白棋2有四口气，白棋3有两口气。

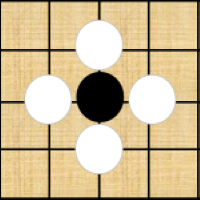
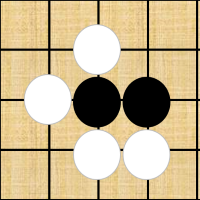
棋子直线紧邻的点上，如果有同色棋子存在，便相互构成一个整体。气也一并计算，如图$（b）$所示，黑棋整体有两口气。 棋子直线紧邻的点上，如果有异色棋子存在，这口气就不复存在。如所有的气均为对方所占据，便呈无气状态，如图$（a）$所示，黑棋无气。无气状态的棋子不能在棋盘上存在，就会被提起。 把无气之子提出盘外的手段叫提子。

a                                    b                                     c

现在给定一盘棋，正好轮到白子下，请问最多能提对方多少黑子？（题目保证初始局面上不存在可以被提的黑子）

5 5
0 0 0 0 0
0 0 1 0 0
0 1 -1 -1 1
0 0 1 1 0
0 0 0 0 0

2